Modelos Baseados em Árvores (Tree-Based Models)

Introdução

Os Modelos Baseados em Árvores (Tree-Based Models) referem-se a todos os algoritmos que utilizam a Árvore de Decisão (Decision Tree) como algoritmo base. Fazem parte destes algoritmos Gradient Boosting, Random Forest e Booststrap Aggregation (Bagging). Internamente, estes algoritmos constroem múltiplas Árvores de Decisão que são combinadas conforme a proposta de cada algoritmo.

Estes algoritmos são empregados para solucionar problemas supervisionados de classificação e regressão. Neste material vamos nos concentrar somente na resolução de um problema de classificação, ilustrando as principais características e vantagens destes algoritmos quando aplicados em conjuntos de dados estruturados.

Independente do algoritmo, todos apresentam métricas de performance muito boas (muitas vezes similares e equivalentes entre eles). O mais importante é prestar atenção em ajustar os hiperparâmetros adequadamente para explorar o máximo de cada algoritmo.

Em especial, Gradient Boosting tem suas variações em termos de pacotes ou framework, por exemplo, Scikit-Learn, XGBoost e CatBoost.

Por fim, vamos explorar uma das características interessantes do CatBoost que simplifica o desenvolvimento e aplicação dos modelos a partir dos algoritmos disponíveis neste framework.

2. Base de Dados

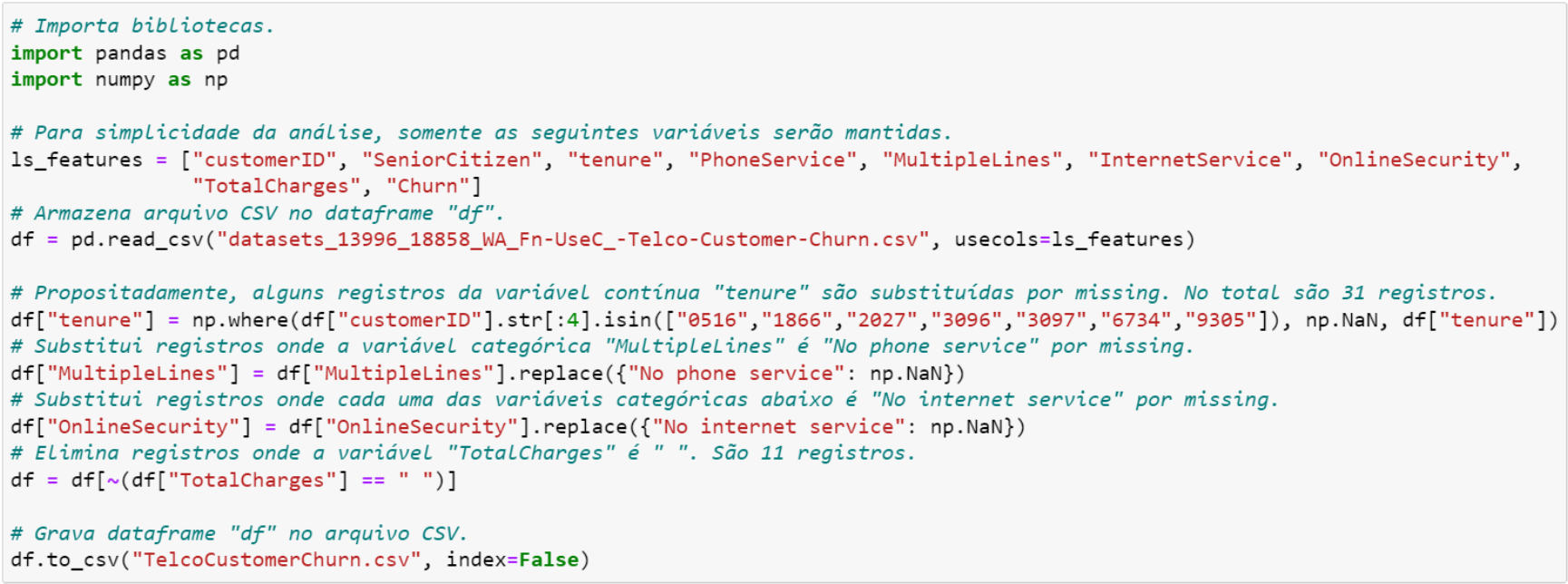
Para explorarmos as principais características e vantagens destes algoritmos, vamos fazer pequenas modificações na base original disponível no Kaggle (vide o link https://www.kaggle.com/datasets/blastchar/telco-customer-churn). As modificações são as seguintes (todas estas modificações podem ser consultadas na Figura 2.1):

• Originalmente, a base de dados tem 21 variáveis. Na base modificada, mantivemos apenas nove variáveis (veja a lista ls_features);
• Selecionamos 31 registros e substituímos os valores originais da variável tenure por valor missing;
• A categoria “No phone service” da variável MultipleLines é substituída por valor missing;
• A categoria “No internet service” da variável OnlineSecurity é substituída por valor missing;
• Eliminamos 11 registros onde TotalCharges é vazio.

Figura 2.1. Base de Dados Modificada

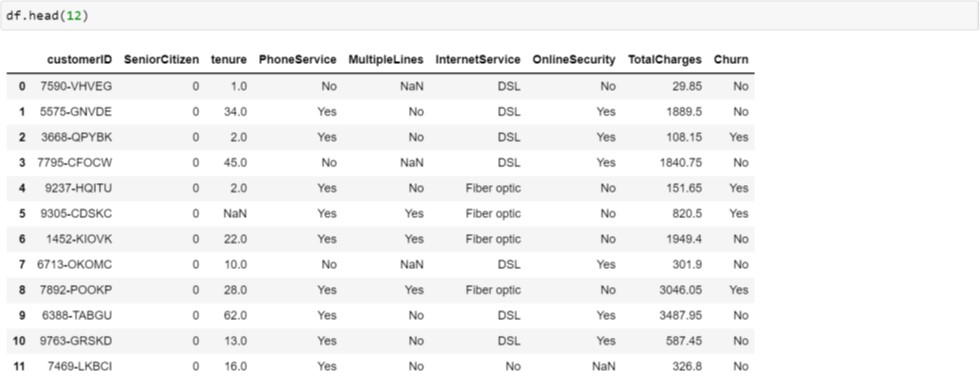
Uma das vantagens destes algoritmos é com relação a valor missing. Por isso, na base modificada inserimos propositadamente valor missing nas variáveis tenure, MultipleLines e OnlineSecurity, o que nos possibilitará a ilustração de procedimentos para lidar com registros nesta situação. A Figura 2.2 mostra como ficou a base modificada.

Figura 2.2. Base de Dados Modificada

3. Principais Vantagens do Modelos Baseados em Árvores

Antes de iniciarmos o desenvolvimento, vamos apresentar algumas das características e vantagens dos Modelos Baseados em Árvores:

• Em geral, a etapa de preparação dos dados é menor que nos demais algoritmos de Aprendizado de Máquina;
• Não tem problema de colinearidade, como nos casos dos modelos paramétricos (por exemplo, Regressão Linear). Um material sobre modelos paramétricos e não paramétricos pode ser visto neste link https://machinelearningmastery.com/parametric-and-nonparametric-machine-learning-algorithms/;
• Independe da escala das variáveis numéricas. Isto significa que não é necessário aplicar transformação das variáveis, tais como padronização ou scaling. Por exemplo, Gradient Boosting é uma construção sequencial de Árvores de Decisão, e este último independe se o valor é absoluto ou normalizado para particionar os nós das árvores, e sim a quantidade de registros que vão em cada nó para o cálculo da RMSE, Gini ou Entropy!
• Em geral, lida muito bem com valores extremos, outliers e valor missing (tanto por omissão ou falta de preenchimento, quanto pelo fato de ser estrutural);
• Adicionalmente, CatBoost lida com variáveis categóricas não numéricas sem a necessidade de dicotomização via get_dummies() ou OneHotEncoder();
• Outra característica específica do CatBoost é lidar com valor missing para variáveis numéricas (contínua e categórica). Assim, o tratamento do valor missing pode ser eliminada da fase de preparação dos dados.

Estas características fazem com que os Modelos Baseados em Árvores se apresentem como opções que simplificam e facilitam a implantação (deployment) dos modelos, entregando modelos com excelente métricas de performance de maneira eficiente e eficaz.

Como principal característica, os Modelos Baseados em Árvores são formados por algoritmos extremamente eficientes. Portanto, é muito importante controlar os hiperparâmetros a fim de evitar overfitting.

4. Gradient Boosting – Scikit-Learn

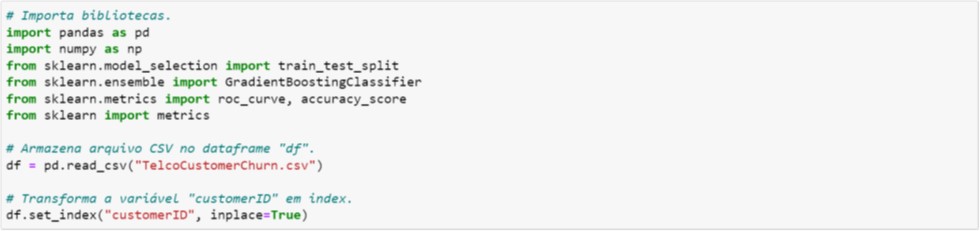
Nesta seção, vamos aplicar o algoritmo Gradient Boosting do pacote Scikit-Learn na base modificada vista na Seção 2. A Figura 4.1 ilustra a importação dos pacotes e em seguida a importação dos dados. Além disso, a variável customerID é transformada em índice.

Figura 4.1. Importação dos pacotes e dos dados

Na Figura 4.2. ilustramos a etapa de preparação dos dados. Em geral, esta é uma etapa que gastamos muito tempo, pois é o momento que exploramos a base toda, procuramos conhecer e analisar a consistência dos dados, identificarmos qualquer anomalia que necessite de um tratamento específico e efetuarmos os ajustes necessários para treinamento do modelo.

Em particular, vamos destacar a forma como nós tratamos o valor missing:

• Em primeiro lugar, é importante conhecer a natureza do valor missing já que em algumas situações podem significar “Não Aplicável”, ou seja, é um missing estrutural. Em outras situações o valor missing é devido a falta de preenchimento ou dado faltante;
• A presença do valor missing na base de dados implica em expurgo do registro inteiro quando treinamos o modelo. Por isso, a importância da imputação ou substituição do valor missing por uma informação válida, pois é um recurso para “salvar” os registros;
• Para uma variável numérica contínua e categórica numérica (desde que seja ordinal) selecionamos um valor fora do intervalo de valores válidos ou observados na variável. Mais especificamente, para variáveis positivas ou não negativas (como é o caso da tenure), utilizamos substituímos pelo valor -1. Na prática, é muito comum substituir valor missing pela média dos valores válidos, ou ainda, aplicar alguma técnica de imputação mais sofisticada. Porém, na Orbis Analytics não seguimos esta prática quando utilizamos os Modelos Baseados em Árvores, pois, entendemos que esta é a melhor prática a ser seguida quando há valor missing na base, independente se o valor missing é devido a dado faltante ou estrutural;
• Para variáveis categóricas não numérica, geralmente tratamos valor missing como sendo uma categoria (substituindo-o adequadamente por um código ou descrição), da mesma forma como fizemos com as variáveis MultipleLines e OnlineSecurity ao atribuí-lo como “SI” (Sem Informação). Em algumas situações raras, quando a frequência do valor missing é muito baixa, agrupamos em uma categoria já existente. Este procedimento dependerá de caso a caso.

Por fim, a variável resposta (target) Churn é convertida em numérica, ou seja, variável dicotômica 1 e 0.

Figura 4.2. Tratamento dos dados

Após os tratamentos, a base é particionada em Treino e Teste sem considerar a variável MonthlyCharges (vide Figura 4.3 que ela não consta da lista ls_features).

Em seguida dicotomização as variáveis categóricas das bases de Treino e de Teste. Repare que o processo de dicotomização é ligeiramente diferente para Treino (X_train) e Teste (X_test). Isto garantirá que, após o processo de dicotomização, a estrutura da base de Teste seja exatamente a mesma da base de Treino. Apesar de parecer desnecessário, este processo é extremamente importante quando a quantidade de categorias de uma variável é diferente entre as bases de Treino e de Teste.

Como consequência, este processo será crítico no deployment, principalmente, no caso de Online Inference Score. Voltaremos com este assunto na Seção 7.

Figura 4.3. Dicotomização e treinamento do modelo

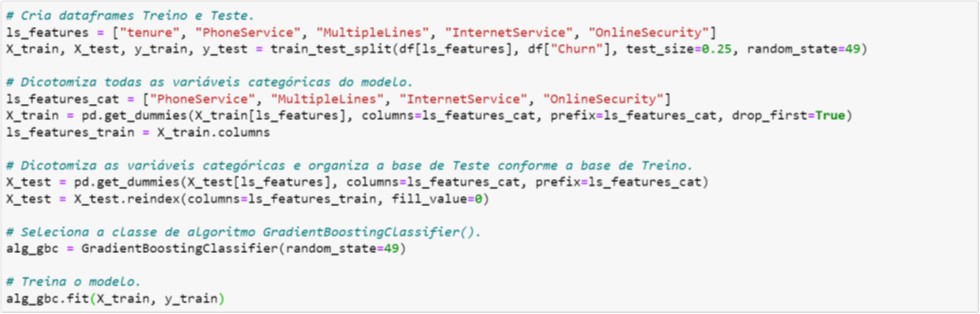
Na parte final da Figura 4.3, o modelo é treinado utilizando algoritmo Gradient Boosting. O hiperparâmetro random_state=49 é para que o leitor possa reproduzir exatamente os resultados contidos neste material.

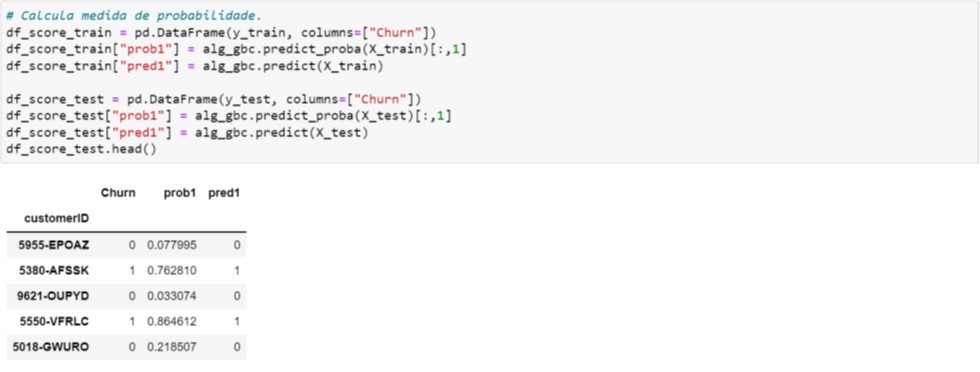
Uma vez treinado o modelo, imprimimos os valores preditos (prob1 e pred1) para os cinco primeiros registros da base de Teste (vide Figura 4.4), onde:

• prob1: probabilidade de Churn;
• pred1: classifica como 1 caso prob1 ≥ 0,5 e 0 quando prob1 < 0,5.

Figura 4.4. Cálculo dos valores preditos

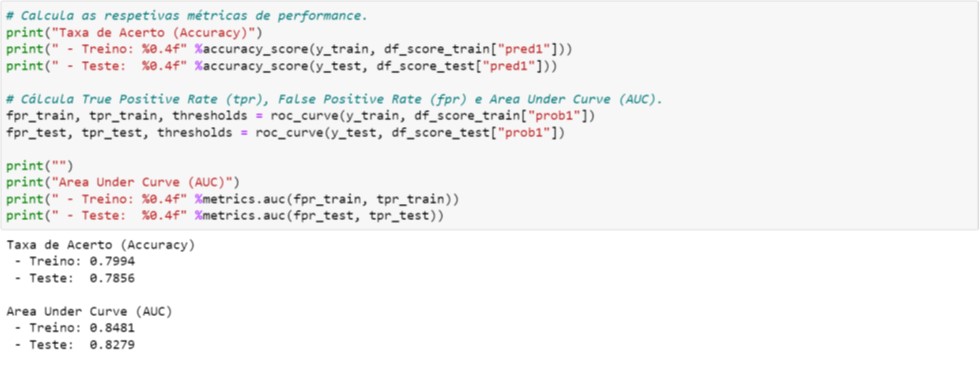
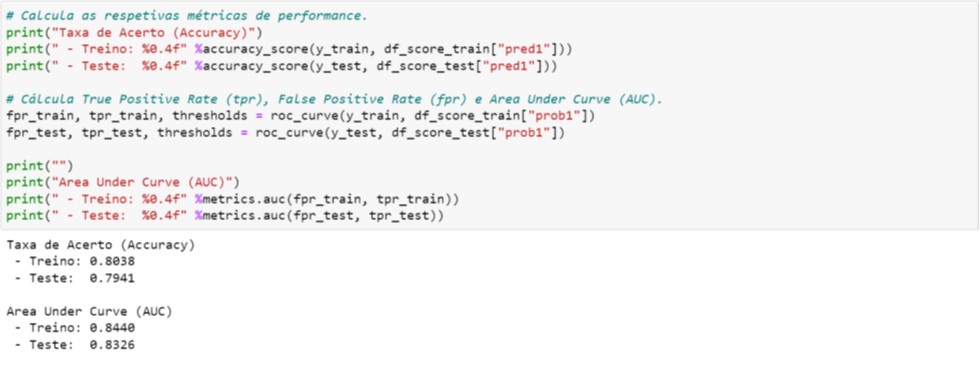
Na Figura 4.5 imprimimos duas métricas de performance: taxa de acerto (accuracy) e AUC (Area Under Curve). Para avaliação dos modelos, na Orbis Analytics analisamos sempre a AUC para avaliar e comparar a performance com outros modelos (outra métrica que utilizamos é o KS, que é o acrônimo de Komogorov-Smirnoff). Somente em situações específicas utilizamos as métricas provenientes da Matriz de Confusão, tais como, accuracy, precision, recall ou F1 Score (em breve, publicaremos um material que explorar as nuances das métricas de performance).

Um dos principais motivos pelo qual analisamos a AUC é o fato de ser uma excelente métrica para avaliar e identificar princípio de overfitting:

• Se a performance da base de Treino for maior que a de Teste, pode indicar princípio de overfitting; portanto, os hiperparâmetros deveriam ser revisados de tal forma que as duas métricas estejam equilibradas;
• Se a performance da base de Treino for menor que a de Teste, indica que há espaço para melhorar o modelo, e para isso, precisamos ajustar os hiperparâmetros adequadamente;
• Ainda que as performances sejam equilibradas, é possível que ajustes pontuais nos hiperparâmetros possam proporcionar melhoria nas métricas de performance.

O processo de ajuste dos hiperparâmetros é conhecido como tuning em Aprendizado de Máquina e pode ser feito manualmente ou utilizando procedimentos como GridSeach e RandomSearch (em breve, falaremos sobre como ajustar os hiperparâmetros através destes procedimentos).

Figura 4.5. Cálculo das métricas de performance

No restante desta Seção, abordaremos os efeitos da padronização dos dados nos Modelos Baseados em Árvore. Na verdade, destacaremos que a padronização das variáveis exploratórias não interfere nos resultados (cálculo da medida de probabilidade e das métricas de performance).

Na ilustração da Figura 4.6 acrescentamos o processo de padronização das bases de Treino e de Teste. Note que optamos por aplicar manualmente a padronização, mas o leitor poderá utilizar as funções StandardScaler() ou MinMaxScaler() já existentes no Scikit-Learn.

Figura 4.6. Padronização dos dados antes do treinamento do modelo

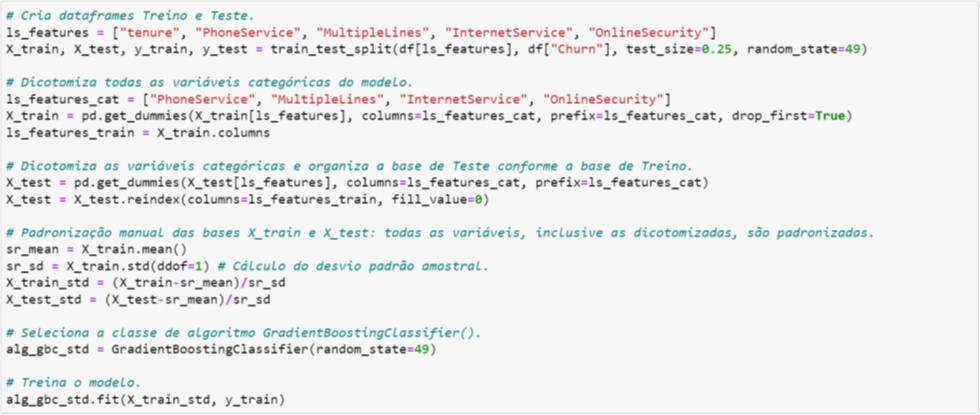
Um ponto de atenção na padronização da base de Teste: primeiramente as médias e desvios-padrão da base de Treino são calculados e em seguida aplicados na base de Teste! Isto garantirá que o valor de uma variável original nas bases de Treino e de Teste tenham o mesmo valor padronizado nas bases padronizadas de Treino e de Teste! Vejamos o seguinte exemplo:

• Suponha um registro na base de Treino e outro registro na base de Teste, ambos com tenure = 8;
• A média e o desvio-padrão (dp) da base de Treino obtidos foram 4 e 10, respectivamente;
• A média e o desvio-padrão (dp) da base de Teste obtidos foram 5 e 12, respectivamente;
• Se a padronização destes dois registros fosse calculada usando os seus respectivos média e desvio-padrão teríamos:

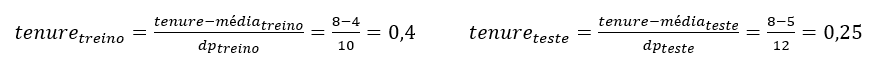
• Note que o valor original 8, quando padronizado, é diferente nas bases de Treino e de Teste (0,4 e 0,25, respectivamente)! Por isso, sempre padronizamos a base de Teste com as estatísticas obtidas da base de Treino;
• Repare que esta situação também aparecerá no deployment. Nos casos de Online Inference, quando uma aplicação recebe um registro de cada vez, qual média e desvio-padrão deveremos utilizar? Um tema para refletir…

Figura 4.7. Cálculo dos valores preditos – Variáveis padronizadas

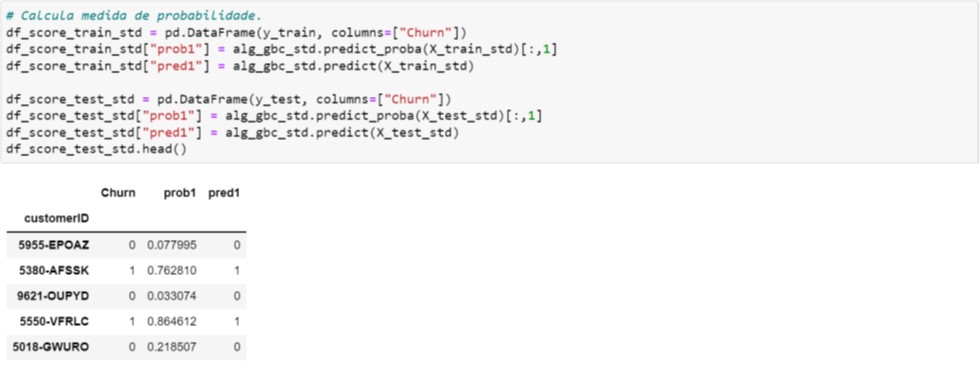
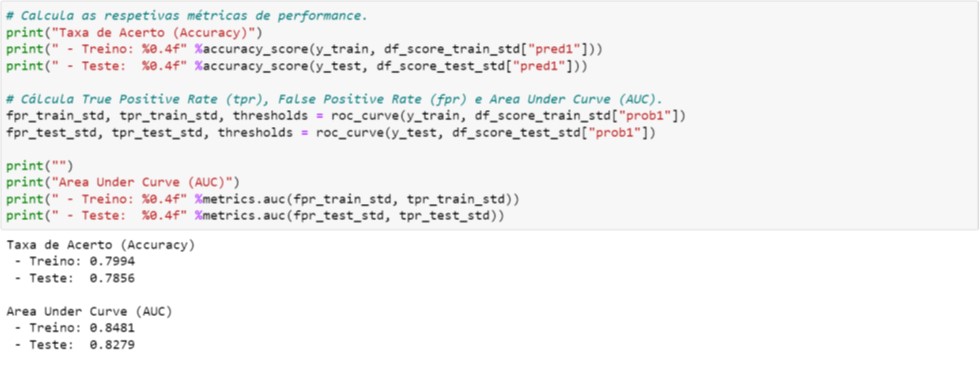
Note que a probabilidade de Churn (prob1 da Figura 4.7) e as métricas de performance (Figura 4.8) são iguais àqueles obtidos utilizando as variáveis originais (vide Figura 4.4 e Figura 4.5, respectivamente).

Com isso, ilustramos que o processo de padronização ou scaling das variáveis exploratórias não interferem ou não tem impacto nos resultados quando utilizamos Modelos Baseados em Árvores.

Figura 4.8. Cálculo das métricas de performance – Variáveis padronizadas

Para finalizar esta Seção, vamos gravar em arquivos todas as informações produzidas durante o treinamento do modelo e que serão necessários durante o processo de deployment (Seção 7). Estes arquivos serão gravados na extensão .pkl (pickle) conforme a Figura 4.9 abaixo:

• pkl: lista todas as variáveis exploratórias da base original que foram selecionadas para desenvolvimento do modelo;
• pkl: lista todas as variáveis exploratórias categóricas que foram dicotomizadas;
• pkl: lista todas as variáveis exploratórias da base final utilizadas para desenvolvimento do modelo
• pkl: objeto que armazena o modelo de Gradient Boosting treinado.

Figura 4.9. Arquivos pickle

Adicionalmente, se a padronização for aplicada durante treinamento do modelo, deveremos armazenar em arquivos .pkl as estatísticas calculadas na base de Treino.

5. Random Forest – Scikit-Learn

Random Forest é um outro algoritmo que faz parte dos Modelos Baseados em Árvores, portanto gera um conjunto de Árvores de Decisão (algoritmo base) que ao final são combinadas para formar um algoritmo mais eficiente. Este algoritmo difere do Gradient Boosting na forma como o conjunto de algoritmo base é combinado, e esta diferença discutiremos isto num outro artigo que será brevemente publicado.

Aqui não reproduziremos todos os passos, mas o leitor poderá substituir GradientBoostingClassifier() por RandomForestClassifier() nas Figura 4.3 e Figura 4.6, respectivamente. Os valores preditos deverão ser os que aparecem na Figura 5.1 (não esquecer de utilizar o hiperparâmetro random_state=49 para reproduzir exatamente os resultados).

Figura 5.1. Cálculo dos valores preditos – Random Forest

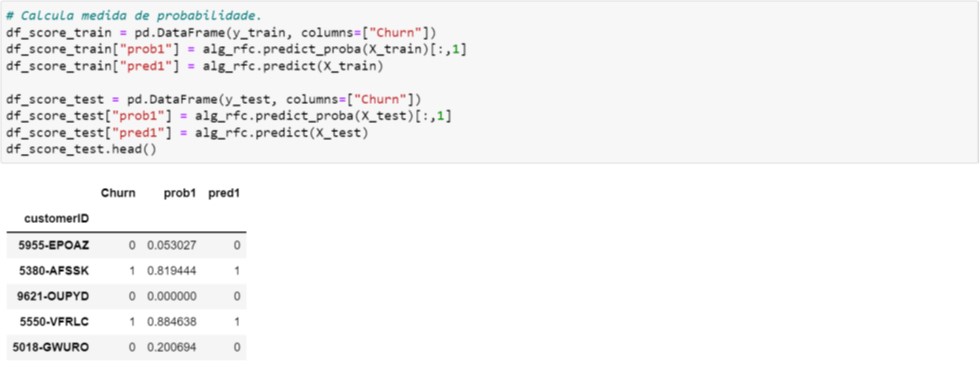
Na Figura 5.2 ilustramos as mesmas métricas de performances apresentadas no Gradient Boosting (vide Figura 4.5 e compare os resultados).

O leitor também é incentivado a utilizar a padronização das variáveis e notará que os resultados serão os mesmos que os obtidos para as variáveis originais.

Figura 5.2. Cálculo das métricas de performance – Random Forest

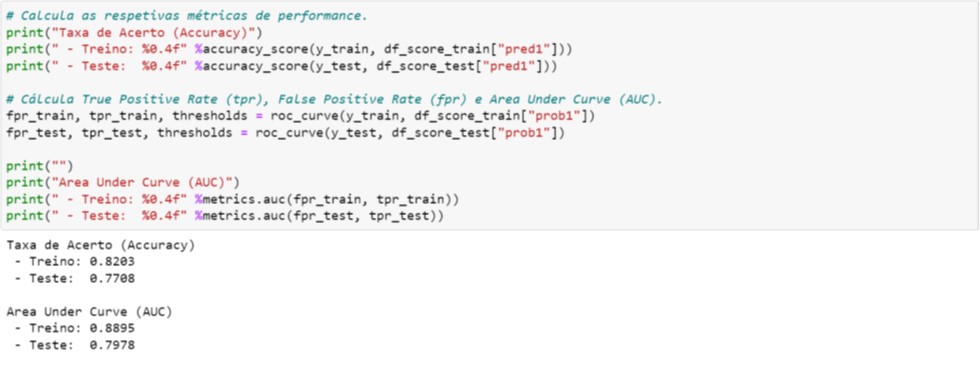
No caso do Random Forest, destacamos um ponto importante: a diferença entre AUC da base de Treino (0,8895) e da base de Teste (0,7978). Na Seção 4 comentamos que pode indicar overfitting do modelo quando a métrica da base de Treino for maior que a da base de Teste. Para Random Forest utilizamos os hiperparâmetros default, assim, deveremos ajustá-los adequadamente a fim de obtermos métricas equilibradas entre ambas as bases. Note que no Gradient Boosting (Figura 4.5) as métricas estão muito próximas! O quadro a seguir ilustra esta comparação:

AUC: Gradient Boosting vs Random Forest utilizando hiperparâmetros default do Scikit-Learn

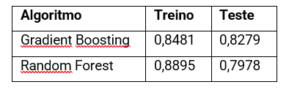
Na prática, a situação descrita acima para Random Forest é muito comum entre os algoritmos dos Modelos Baseados em Árvores. Isto porque estes algoritmos são extremamente eficientes, por isso, devemos sempre analisar, avaliar e comparar as métricas de performance tanto na base de Treino quanto na base de Teste.

Assim, ao avaliarmos a performance pela base de Teste, diríamos que Gradient Boosting gerou um modelo superior ao do Random Forest. Isto não é necessariamente verdade, já que na base de Treino a performance do Random Forest foi superior! Ou seja, Random Forest gerou um modelo (tão bom) que não consegue reproduzir a mesma performance na base de Teste.

Uma das formas para diminuir a diferença entre as performances das bases de Treino e de Teste (e assim, evitar overfitting) é ajustar adequadamente os hiperparâmetros ao diminuir a performance da base de Treino. Como consequência, geralmente a performance da base de Teste aumentará.

Conforme já mencionamos na Seção 1, ao ajustar adequadamente seus respectivos hiperparâmetros todos os algoritmos que pertencem a Modelos Baseados em Árvores entregam performances similares e equivalentes!

6. CatBoost

CatBoost é um framework relativamente novo comparado com XGBoost ou com o pacote Scikit-Learn. Neste material, exploraremos algumas características adicionais e interessantes:

• Por default, valor missing das variáveis numéricas (contínuas ou categóricas ordinais) é substituído pelo valor mínimo fora do intervalo de valores válidos (veja outras opções no link https://catboost.ai/en/docs/concepts/algorithm-missing-values-processing). CatBoost não lida com valor missing no caso de variáveis categóricas não numéricas;
• A não necessidade da dicotomização das variáveis categóricas não numéricas.

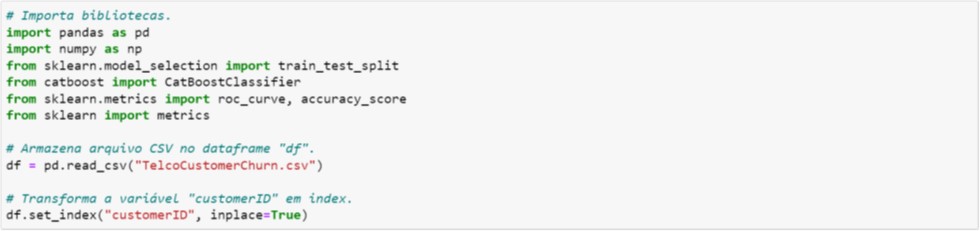
Nesta Seção vamos seguir os mesmos passos do Gradient Boosting. Assim, na Figura 6.1 ilustramos a importação dos pacotes e em seguida a importação dos dados. A única diferença em relação a Figura 4.1 é a importação do algoritmo.

Figura 6.1. Importação dos pacotes e dos dados

Na Figura 6.2, após a partição da base em Treino e Teste, note que não há necessidade do processo de dicotomização. Apenas devemos informar quais são as variáveis categóricas não numéricas (ls_features_cat).

Figura 6.2. Tratamento dos dados e treinamento do modelo

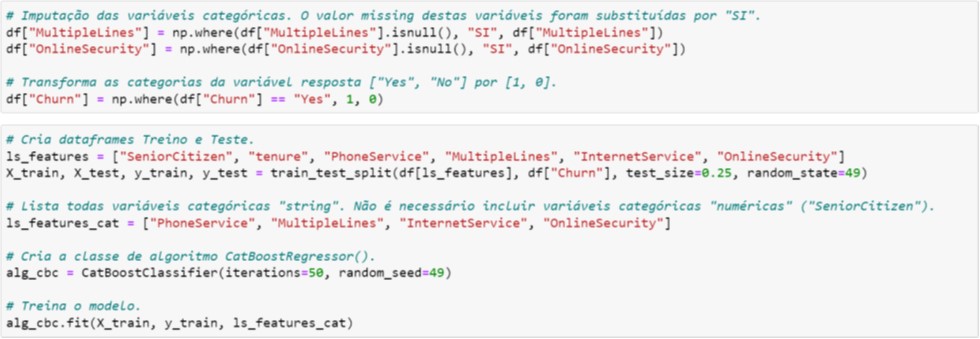
Por default, o hiperparâmetro iterations=1000 (isto significa que são construídas 1.000 árvores de decisão!). Para evitarmos overfitting, selecionamos valor um valor conservador, ou seja, iterations=50.

Na Figura 6.3, calculamos os valores preditos e imprimimos os cinco primeiros registros da base de Teste.

Figura 6.3. Cálculo dos valores preditos – CatBoost

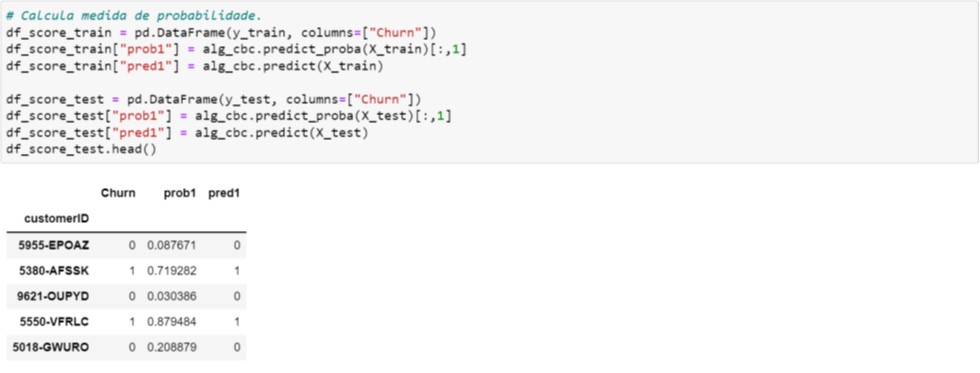
Na Figura 6.4 imprimimos as duas métricas de performance. Ao compararmos a AUC da base de Teste com aquela obtida no Gradiente Boosting do Scikit-Learn, notamos que a performance é ligeiramente superior. Nos nossos testes e aplicações, a performance do CatBoost sistematicamente tem apresentado esta ligeira superioridade.

Figura 6.4. Cálculo das métricas de performance – CatBoost

Por fim, o único arquivo (extensão .cbm) que precisamos gravar é aquele que armazenará o modelo de Gradient Boosting treinado, conforme Figura 6.5.

Figura 6.5. Gravação do modelo – CatBoost

Conforme mencionamos no início desta Seção, CatBoost traz estas características e funcionalidades adicionais que simplificam algumas etapas do treinamento, e principalmente aproveita esta simplicidade no processo de deployment, assunto da próxima Seção.

7. Deployment

Nesta Seção, vamos aplicar os modelos de Gradient Boosting treinados através do pacote Scikit-Learn (Seção 4) e do framework CatBoost (Seção 6).

No sentido mais amplo, deployment significa colocar o modelo treinado em produção ou criar um aplicativo através dele. Veja dois exemplos simples de aplicativos no nosso site (https://orbisanalytics.com.br/aplicacoes). Neste material, vamos referir deployment à apenas “aplicação de dados novos” aplicando os modelos treinados. Em geral, denominamos este processo de scoring, que será basicamente o cálculo da probabilidade de Churn.

Na Figura 7.1 ilustramos todos os pacotes necessários para o processo de scoring, tanto para Scikit-Learn quanto para CatBoost. Além dos pacotes, é necessário carregar todos os arquivos gravados durante o desenvolvimento dos modelos.

Figura 7.1. Importação dos pacotes e dos modelos

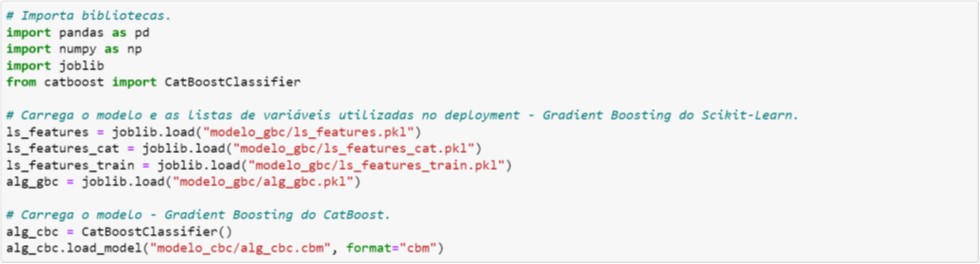
Na prática, trabalhamos com apenas um modelo e em geral aquele com a melhor métrica de performance. Portanto, se a escolha for pelo modelo de Gradient Boosting não é necessário carregar o modelo CatBoost, e vice-versa. Na ilustração acima carregamos ambos os modelos apenas com intuito de explorar as diferenças no processo de scoring.

O próximo passo é selecionar os dados brutos (são dois registros representado pelo dicionário dados da Figura 7.2) que passarão pelo mesmo processo de tratamento aplicado durante treinamento do modelo.

Figura 7.2. Tratamento dos dados

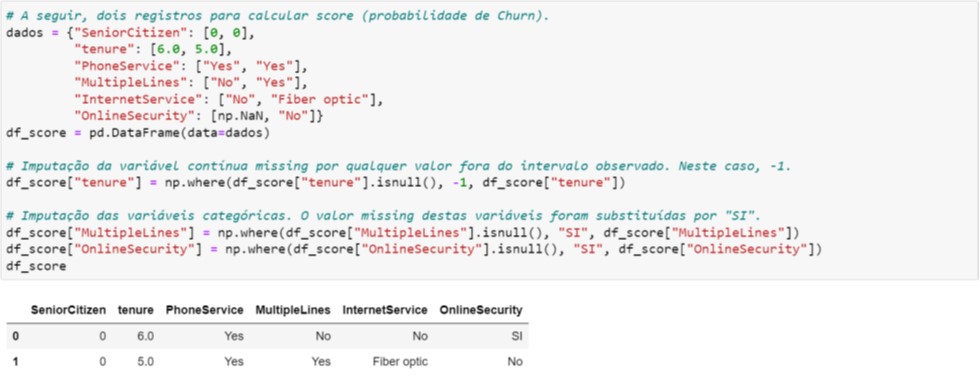
A partir da base tratada ilustraremos a diferença no processo de scoring entre os modelos de Gradient Boosting do Scikit-Learn e CatBoost.

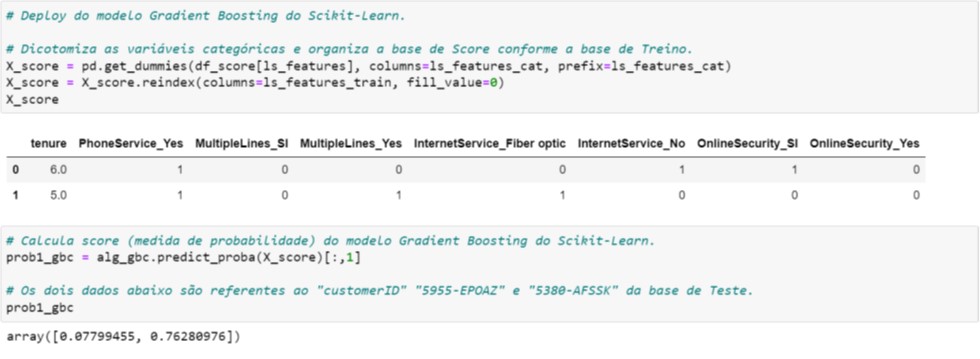
Começaremos pelo Scikit-Learn (Figura 7.3). Note que durante o processo de dicotomização, utilizamos as listas de variáveis carregadas no início do script (vide Figura 7.1). Isto garantirá que a estrutura da base (X_score) seja a mesma da base utilizada no treinamento (X_train; vide Figura 4.3).

Por fim, aplicamos o modelo nesta base transformada e obtemos a probabilidade de Churn para os dois registros. Estes registros são justamente os dois primeiros registros da base de Teste (confira na Figura 4.4).

Figura 7.3. Processo de scoring – Scikit-Learn

No CatBoost não aplicamos a dicotomização nas variáveis categóricas durante o treinamento do modelo. Portanto, isto simplifica o processo de scoring conforme ilustramos na Figura 7.4.

Figura 7.4. Processo de scoring – CatBoost

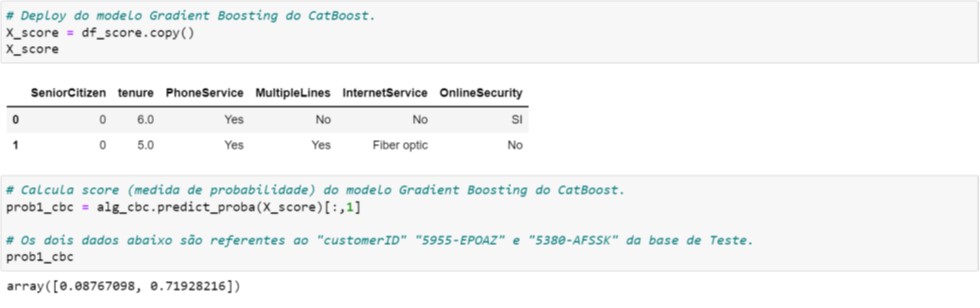
O cálculo da probabilidade de Churn destes dois registros é igual àquele que consta da Figura 6.3.

8. Regressão

Todas os passos apresentados neste artigo também podem ser aplicados para regressão. Em breve publicaremos material similar para regressão, mas enquanto isso, sugerimos ao leitor interessado que faça as seguintes modificações nos códigos apresentados neste material:

• Substitua a variável resposta Churn por TotalCharges e utilizar as mesmas variáveis exploratórias;
• Substitua o algoritmo GradientBoostingClassifier() por GradientBoostingRegressor();
• Substitua o algoritmo RandomForestClassifier() por RandomForestRegressor();
• Substitua o algoritmo CatBoostClassifier() por CatBoostRegressor();
• Com relação às métricas de performance a sugestão é utilizar RMSE (root mean squared error) e R² (coeficiente de determinação).

9. Conclusão

Principalmente para os leitores que estão iniciando, vale a pena testar os diferentes algoritmos disponíveis, identificar aqueles que entregam boas performances e selecionar um com a qual se sente mais confortável.

Em se tratando de Modelos Baseados em Árvores, são algoritmos de desenvolvimento rápido e eficazes, principalmente quando lidamos com dados estruturados, além das características e vantagens apresentadas na Seção 3.

Especialmente, apresentamos características adicionais do CatBoost, simplificando ainda mais o processo de treinamento do modelo (Seção 6) e do deployment (Seção 7). Isto porque no Scikit-Learn (e em geral nos demais pacotes e frameworks) o processo de dicotomização durante o treinamento do modelo é necessário quando há variáveis categóricas não numéricas! Isto porque as bases X_train e X_test obrigatoriamente são preenchidos por elementos numéricos, e o processo natural para isso é a dicotomização em 1 e 0 das categorias das variáveis categóricas.

No CatBoost, a dicotomização é desnecessária, ou seja, as bases X_train e X_test podem conter variáveis categóricas não numéricas, bastando informá-lo apenas quais são estas variáveis durante o treinamento do modelo.

Em nossa experiência, apesar da diferença ser pequena, sistematicamente CatBoost tem apresentado métricas de performance ligeiramente superior aos demais algoritmos/frameworks.

Todos os conceitos e procedimentos apresentados neste material são trabalhados em nos nossos treinamentos. Consulte no link https://orbisanalytics.com.br/treinamento/ ou contate nos para mais informações.